9. Blocksim

tbcontrol.blocksim is a simple library for simulating the kinds of block diagrams you would encounter in a typical undergraduate control textbook. Let’s start with the most basic example of feedback control.

import tbcontrol
tbcontrol.expectversion("0.1.1")

from tbcontrol import blocksim

Our first job is to define objects representing each of the blocks. A common one is the LTI block

Gp = blocksim.LTI('Gp', 'u', 'y', 10, [100, 1], 50)

Gp

LTI: u →[ Gp ]→ y

We’ll use a PI controller

Gc = blocksim.PI('Gc', 'e', 'u', 0.1, 50)

Gc

PI: e →[ Gc ]→ u

Once we have the blocks, we can create a Diagram.

Sums are specified as a dictionary with the keys being the output signal and the values being a tuple containing the input signals. The leading + is compulsory.

The inputs come next and are specified as functions of time. Blocksim.step() can be used to build a step function.

diagram = blocksim.Diagram([Gp, Gc],
                           sums={'e': ('+ysp', '-y')},
                           inputs={'ysp': blocksim.step()})

diagram

LTI: u →[ Gp ]→ y
PI: e →[ Gc ]→ u

Blocksim is primarily focused on being able to simulate a diagram. The next step is to create a time vector and do the simulation.

import numpy

The time vector also specifies the step size for integration. Since blocksim uses Euler integration internally you should choose a time step which is at least 10 times smaller than the smallest time constant of all the blocks. The timespan is of course dependent on what you are investigating.

ts = numpy.arange(start=0, stop=1000, step=1)

simulation_results = diagram.simulate(ts, progress=True)

The result of simulate() is a dictionary containing the simulation results.

import matplotlib.pyplot as plt

%matplotlib inline

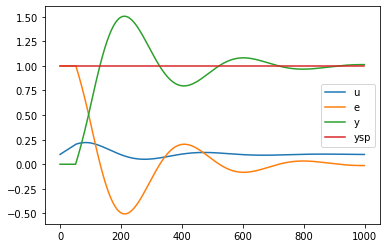
for signal, value in simulation_results.items():
    plt.plot(ts, value, label=signal)
plt.legend()

<matplotlib.legend.Legend at 0x1c19f872b0>

9.1. Re-using parts of a diagram

Let’s compare the output of a PI and a PID controller on this system. We’ve already got the PI response, which we should store.

y_pi = simulation_results['y']

Let’s swap out the PI controller for a PID.

Gc_pid = blocksim.PID('Gc', 'e', 'u', 0.1, 50, 25)

diagram.blocks = [Gp, Gc_pid]

simulation_results = diagram.simulate(ts, progress=True)

plt.plot(ts, y_pi, label='PI')
plt.plot(ts, simulation_results['y'], label='PID')
plt.legend()

<matplotlib.legend.Legend at 0x1c1a113d68>

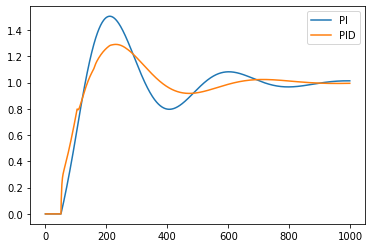
We can see that adding the derivative action has improved control.

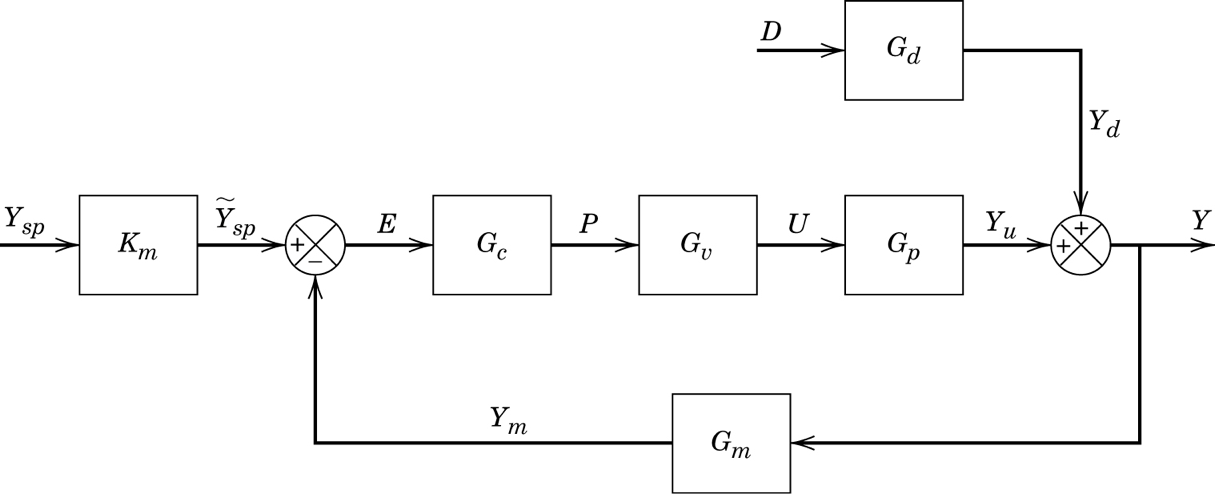
10. Disturbances

We can simulate a more complicated block diagram with a disturbance.

Km = blocksim.LTI('Km', 'ysp', 'ytildesp', 1, 1)
Gc = blocksim.PI('Gp', 'e', 'p', Kc=8, tau_i=10)
Gv = blocksim.LTI('Gv', 'p', 'u', 1, 1)
Gp = blocksim.LTI('Gp', 'u', 'yu', [1], [10, 1])
Gd = blocksim.LTI('Gd', 'd', 'yd', [1], [10, 1])
Gm = blocksim.LTI('Gm', 'y', 'ym', [1], [1, 1])

blocks = [Km, Gc, Gv, Gp, Gd, Gm]

sums = {'e': ('+ytildesp', '-ym'),
        'y': ('+yd', '+yu')}

inputs = {'ysp': blocksim.step(),
          'd': blocksim.step(starttime=50)}

diagram = blocksim.Diagram(blocks, sums, inputs)

ts = numpy.arange(start=0, stop=100, step=0.05)

results = diagram.simulate(ts, progress=True)

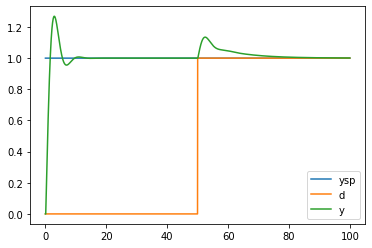
for name in ('ysp', 'd', 'y'):
    plt.plot(ts, results[name], label=name)
plt.legend()

<matplotlib.legend.Legend at 0x1c19feccf8>

11. Algebraic equations

Sometimes it is useful to be able to handle non-linear calculations in block diagrams. This deviates from the strict interpretation of block diagrams but can be useful for instance in calculating the response of a controller with output limits.

import numpy

def limit(t, u):
    return numpy.clip(u, 0, 0.2)

Gp = blocksim.LTI('Gp', 'ulimited', 'y', 10, [100, 1], 50)
Gc = blocksim.PI('Gc', 'e', 'u', 0.1, 50)

limiter = blocksim.AlgebraicEquation('Limiter', 'u', 'ulimited', limit)

diagram = blocksim.Diagram([Gp, Gc, limiter],
                           sums={'e': ('+ysp', '-y')},
                           inputs={'ysp': blocksim.step()})

ts = numpy.arange(start=0, stop=1000, step=1)

simulation_results = diagram.simulate(ts)

diagram

LTI: ulimited →[ Gp ]→ y
PI: e →[ Gc ]→ u
AlgebraicEquation: u →[ Limiter ]→ ulimited

plt.plot(ts, simulation_results['u'])
plt.plot(ts, simulation_results['ulimited'])

[<matplotlib.lines.Line2D at 0x1c1a16ad68>]

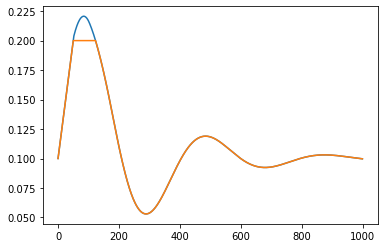
We can see the effect of the limiter clearly in the above figure