9. Closed loop controlled responses

I discuss drawing these response qualitatively in this video. Note that the responses that are drawn in the video match the responses drawn here, but the value of \(\tau_I\) specified there doesn’t show overshoot as in this notebook. The value in the video is \(\tau_I=10\), but that was obviously a bit too large to allow for the extreme oscillation. You can get a similar response to the one I sketched by using \(\tau_I=1\). The value below has been chosen to make the discussion in the video still hold in the same way.

from tbcontrol.loops import feedback
import control
import matplotlib.pyplot as plt
import numpy
%matplotlib inline

s = control.tf([1, 0], 1)

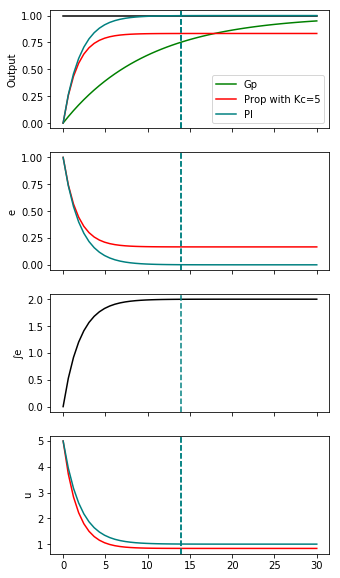
Gp = 1/(10*s + 1)
PI = 5*(1 + 1/(10*s))
P = 5

ts = numpy.linspace(0, 30)

Find the time where the error becomes zero by interpolating on the output response

t, y = control.step_response(feedback(PI*Gp, 1))
errorzero = numpy.interp(1, y, t)

This function will plot a response for us

def plotresponse(ax, G, *args, **kwargs):
    ax.plot(*control.step_response(G, T=ts), *args, **kwargs)
    ax.axvline(errorzero, color='teal', linestyle='--')

I’m trying to get all the colors to match the video here.

fig, (outputs, errors, errorint, u) = plt.subplots(4, 1, figsize=(5, 10), sharex=True)
outputs.plot(ts, numpy.ones_like(ts), color='black')
plotresponse(outputs, Gp, color='green', label='Gp')
plotresponse(outputs, feedback(P*Gp, 1), color='red', label='Prop with Kc=5')
plotresponse(outputs, feedback(PI*Gp, 1), color='teal', label='PI')
outputs.set_ylabel('Output')
outputs.legend()

plotresponse(errors, 1 - feedback(P*Gp, 1), color='red')
plotresponse(errors, 1 - feedback(PI*Gp, 1), color='teal')
errors.set_ylabel('e')

plotresponse(u, feedback(P, Gp), color='red')
plotresponse(u, feedback(PI, Gp), color='teal')
u.set_ylabel('u')

plotresponse(errorint, (1 - feedback(PI*Gp, 1))/s, color='black')
errorint.set_ylabel('∫e');