4. Dahlin controller
We will replicate the controller output in figure 17.11a. This notebook has a video commentary.
Note I am replicating these results using analytic methods to show that the artefacts are not numerical but rather fundamental to the calculations. If you simply want to simulate the action of a discrete controller on a continuous system, have a look at the Simple discrete controller simulation notebook.
[1]:
import sympy
sympy.init_printing()
import tbcontrol
tbcontrol.expectversion('0.1.3')
5. Discretise the system
We need to find the corresponding z transform of the hold element and the system. Since \(H=1/s(1 - e^{-Ts})\), we can find \(F=G/s\), from there \(f(t)\) and then work out the \(z\) transform
[2]:
s, t = sympy.symbols('s, t')
Gs = 1/(15*s**2 + 8*s + 1)
Gs
[2]:
[3]:
f = sympy.inverse_laplace_transform(Gs/s, s, t).simplify()
sympy.nsimplify(sympy.N(f)).simplify()
[3]:
We can see that \(f(t)\) is the sum of 1 and two exponentials. It is easy to determine the corresponding z transforms from the table
Time domain |
Laplace-transform |
z-transform (\(b=e^{-aT}\)) |
|---|---|---|
\(e^{-at}\) |
\(\frac{1}{s+a}\) |
\(\frac{1}{1-bz^{-1}}\) |
[4]:
z, q = sympy.symbols('z, q')
Now the sampling interval
[5]:
T = 1 # Sampling interval
[5]:
def expz(a):
b = sympy.exp(-a*T)
return 1/(1 - b*z**-1)
[6]:
Fz = -5/2*expz(1/5) + 3/2*expz(1/3) + 1/(1 - z**-1)
[7]:
Fz
[7]:
Let’s see if we did that right
[8]:
import tbcontrol.symbolic
[9]:
def plotdiscrete(fz, N):
values = tbcontrol.symbolic.sampledvalues(fz, z, N)
times = [n*T for n in range(N)]
plt.stem(times, values)
[10]:
import matplotlib.pyplot as plt
%matplotlib inline
[11]:
import numpy
[12]:
ts = numpy.linspace(0, 10, 300)
[13]:
plotdiscrete(Fz, 10)
plt.plot(ts, tbcontrol.symbolic.evaluate_at_times(f, t, ts))
[13]:
[<matplotlib.lines.Line2D at 0x1205b3ef0>]
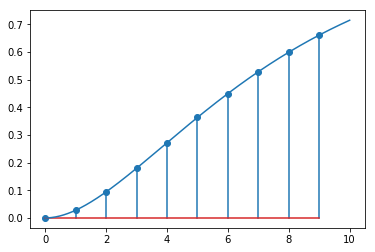
Here is the transform of the system and the hold element. See the Discrete control notebook for the derivation.
[14]:
HG_z = Fz*(1 - z**-1)
6. Dahlin Controller
The desired closed loop response is first order
[15]:
θ = 0 # system dead time
λ = 1 # Dahlin's lambda
h = θ # Dahlin's h
First order response in eq 17-63
[16]:
N = θ/T
A = sympy.exp(-T/λ)
yclz = (1 - A)*z**(-N-1)/(1 - A*z**-1)
[17]:
K = (1/HG_z*yclz/(1 - yclz)).simplify()
[18]:
K
[18]:
[19]:
#K = 0.632/(1 - z*-1) * (1 - 1.5353*z**-1 + 0.5866*z**-2)/(0.028 + 0.0234*z**-1)
We will model the control response to a unit step in reference signal
[20]:
rz = 1/(1 - z**-1) # unit step in z
Now we can calculate the z-domain version of the controller output
[21]:
uz = K/(1 + K*HG_z)*rz
[22]:
N = 10
[23]:
plotdiscrete(uz, N)
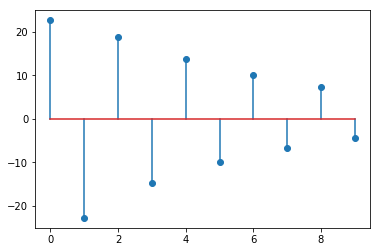
This oscillating controller output is known as “ringing”. It is an undesirable effect.
7. Continuous response
By design the controlled variable follows an exponential at the sampling points.
[24]:
yz = K*HG_z/(1 + K*HG_z)*rz
[25]:
plotdiscrete(yz, N)
plt.plot(ts, 1 - numpy.exp(-ts/λ))
[25]:
[<matplotlib.lines.Line2D at 0x120c51390>]

But what does it really look like between data points? First, let’s construct the response of the system to a single sampling time length pulse input
[26]:
p = f - f.subs(t, t-T)
Note that there is a slight issue with finding the value of this function at zero, so we avoid that point in plotting by starting at some small value which is not zero.
[27]:
smallvalue = 0.001
[28]:
sympy.plot(p, (t, smallvalue, 10))
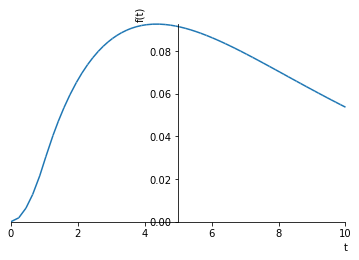
[28]:
<sympy.plotting.plot.Plot at 0x1209627f0>
Let’s get the values of the controller output as a list:
[29]:
u = tbcontrol.symbolic.sampledvalues(uz, z, N)
Now, we calculate the output of the system as the sum of the various pulse inputs.
[30]:
yt = numpy.zeros_like(ts)
for i in range(0, N):
yt += [float(sympy.N(u[i]*p.subs(t, ti-i + smallvalue))) for ti in ts]
Finally, we present the discrete system response, the designed response and the analytical continuous response on the same graph.
[31]:
plotdiscrete(yz, 10)
plt.plot(ts, 1 - numpy.exp(-ts/λ))
plt.plot(ts, yt)
[31]:
[<matplotlib.lines.Line2D at 0x12126f8d0>]
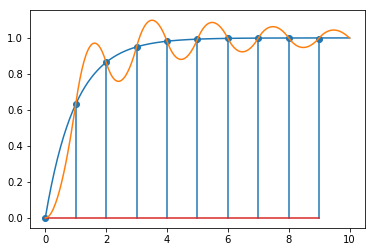
[ ]: