2. First order systems
[1]:
import sympy
import matplotlib.pyplot as plt
import numpy
sympy.init_printing()
%matplotlib inline
[2]:
t, K, tau = sympy.symbols('t, K, tau',real=True, positive=True)
s = sympy.Symbol('s')
[3]:
u = sympy.Heaviside(t)
[4]:
def L(f):
return sympy.laplace_transform(f, t, s, noconds=True)
def invL(F):
return sympy.inverse_laplace_transform(F, s, t)
[5]:
U = L(u)
U
[5]:
All first order linear differential equations with constant coefficients can be rewritten in the following form:
Where \(y\) is the output and \(u\) is the input or forcing function.
If we Laplace transform this, we end up with
\begin{align} \mathcal{L}\left\{\frac{\mathrm{d}y}{\mathrm{d}t}\right\} &= \mathcal{L}\{ay(t) + bu(t)\} \\ sy(s) &= ay(s) + bu(s) \\ y(s) &= \frac{b}{s - a}u(s) \\ \end{align}
By convention, we usually rewrite the above in the following form, for reasons which will become apparent soon:
[6]:
G = K/(tau*s + 1)
G
[6]:
The inverse laplace of a transfer function is its impulse response
[7]:
impulseresponse = invL(G)
impulseresponse
[7]:
If \(u(t)\) is the unit step function, \(U(s)=\frac{1}{s}\) and we can obtain the step response as follows:
[8]:
u = 1/s
stepresponse = invL(G*u)
[9]:
stepresponse
[9]:
Ramp response:
[10]:
u = 1/s**2
rampresponse = invL(G*u)
rampresponse
[10]:
[11]:
from ipywidgets import interact
[12]:
evalfimpulse = sympy.lambdify((K, tau, t), impulseresponse, 'numpy')
evalfstep = sympy.lambdify((K, tau, t), stepresponse, 'numpy')
evalframp = sympy.lambdify((K, tau, t), rampresponse, 'numpy')
[13]:
ts = numpy.linspace(0, 10)
def firstorder(tau_in, K_in):
plt.figure(figsize=(12, 6))
ax_impulse = plt.subplot2grid((2, 2), (0, 0))
ax_step = plt.subplot2grid((2, 2), (1, 0))
ax_complex = plt.subplot2grid((2, 2), (0, 1), rowspan=2)
ax_impulse.plot(ts, evalfimpulse(K_in, tau_in, ts))
ax_impulse.set_title('Impulse response')
ax_impulse.set_ylim(0, 10)
tau_height = 1 - numpy.exp(-1)
ax_step.set_title('Step response')
ax_step.plot(ts, evalfstep(K_in, tau_in, ts))
ax_step.axhline(K_in)
ax_step.plot([0, tau_in, tau_in], [K_in*tau_height]*2 + [0], alpha=0.4)
ax_step.text(0, K_in, '$K=${}'.format(K_in))
ax_step.text(0, K_in*tau_height, '{:.3}$K$'.format(tau_height))
ax_step.text(tau_in, 0, r'$\tau={:.3}$'.format(tau_in))
ax_step.set_ylim(0, 10)
ax_complex.set_title('Poles plot')
ax_complex.scatter(-1/tau_in, 0, marker='x', s=30)
ax_complex.axhline(0, color='black')
ax_complex.axvline(0, color='black')
ax_complex.axis([-10, 10, -10, 10])
[14]:
firstorder(1., 10.)
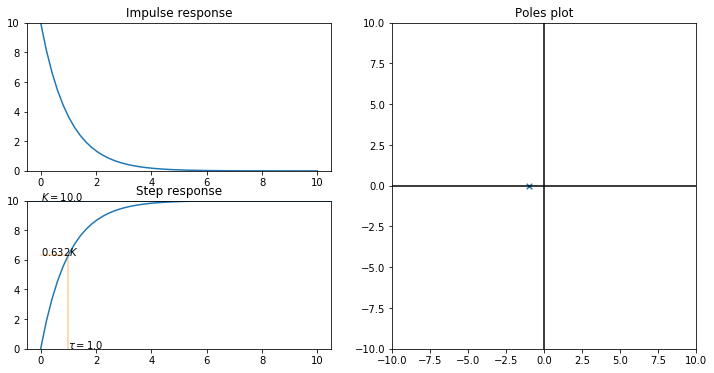
[15]:
interact(firstorder, tau_in=(0.1, 10.), K_in=(0.1, 10.));
Exploration of the above interaction allows us to see the following:
\(K\) scales the response in the \(y\) direction
\(\tau\) scales the response in the \(t\) direction
The response of the system is always \(0.63K\) when \(t=\tau\)
We get the “magic number” 0.63 by substituting \(t=\tau\) into the response:
[16]:
sympy.N((stepresponse.subs(t, tau)/K).simplify())
[16]: