8. A discrete controller class

Let’s extend the example from our previous object-oriented simulation notebook to discrete controllers.

import numpy
import scipy.signal
import matplotlib.pyplot as plt
%matplotlib inline

We start by defining a class for the tank system again:

class TankSystem:
    def __init__(self, A, alpha, K, V, Fi):
        """ This special function gets called when an object of this class is created"""
        self.A = A
        self.alpha = alpha
        self.K = K
        self.Fi = Fi
        self.change_state(V)

    def f(self, x):
        return self.alpha**(x - 1)

    def change_input(self, x):
        self.Fo = self.K*self.f(x)*numpy.sqrt(self.h)

    def change_state(self, V):
        self.state = self.V = V
        self.output = self.h = self.V/self.A

    def derivative(self, x):
        self.change_input(x)
        dVdt = self.Fi - self.Fo
        return dVdt

But this time we’ll do a discrete controller:

class DiscreteController:
    def __init__(self, DeltaT, Kc, tau_i, bias):
        self.DeltaT = DeltaT
        self.Kc = Kc
        self.tau_i = tau_i
        self.next_sample_time = 0
        self.error_sum = 0
        self.bias = self.output = bias

    def update(self, u, t):
        if t >= self.next_sample_time:
            self.error_sum += u
            self.output = self.Kc*(u + 1/self.tau_i*self.error_sum)
            self.next_sample_time += self.DeltaT

I’ve changed the way we update the controller here to accomodate the fact that discrete controllers don’t have states to integrate, so we don’t need the derivative method. The way I’ve built this class requires that the update method be called with strictly ascending times in t. Note that this class corresponds very closely to a physical box. All the sampling is taking place inside the class and it is designed to be updated in a “normal” Euler integration loop. See how using classes makes the calculations which are about a particular physical object (the controller) stay together in the code rather than being spread out in lots of places?

Of course, we still have to test that this works:

ts = numpy.linspace(0, 100, 1000)
dt = ts[1]

sp = 1.3

I’ve changed this function to use the new update methods, but otherwise it is similar to the previous one.

def control_simulation_discrete(system, controller):
    outputs = []
    for t in ts:
        system.change_input(controller.output)

        e = sp - system.output

        controller.update(e, t)

        system.change_state(system.state + system.derivative(controller.output)*dt)

        outputs.append(system.output)
    return outputs

system = TankSystem(A=2, alpha=20, K=2, V=2, Fi=1)
controller = DiscreteController(DeltaT=1, Kc=-1, tau_i=5, bias=0.7)

outputs = control_simulation_discrete(system, controller)

plt.plot(ts, outputs)

[<matplotlib.lines.Line2D at 0x10cf877f0>]

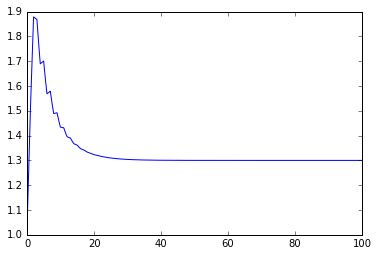
We can still simulate different situations easily.

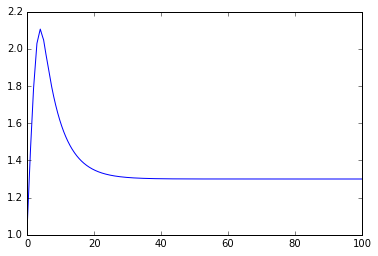
outputs = control_simulation_discrete(system=TankSystem(A=2, alpha=10, K=2, V=2, Fi=1),
                                      controller=DiscreteController(DeltaT=1, Kc=-0.5, tau_i=5, bias=0.5))
plt.plot(ts, outputs);