3. Simplifying block diagrams
These notes detail some techniques for reducing block diagrams graphically. In this notebook, I will solve the problem using SymPy.
Let’s reduce this big block diagram to one input-output relationship (Example 4 in the notes linked to above):
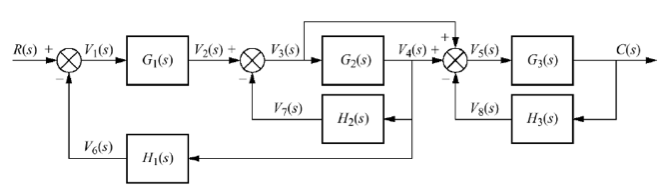
[1]:
import sympy
sympy.init_printing()
[2]:
(R, V1, V2, V3, V4, V5, V6, V7, V8, C,
G1, G2, G3, H1, H2, H3) = sympy.symbols('R, V1, V2, V3, V4, V5, V6, V7, V8, C,'
'G1, G2, G3, H1, H2, H3')
unknowns = V1, V2, V3, V4, V5, V6, V7, V8, C
[3]:
eqs = [# Blocks
V2 - G1*V1,
V4 - G2*V3,
C - G3*V5,
V6 - H1*V4,
V7 - H2*V4,
V8 - H3*C,
# Sums
V1 - (R - V6),
V3 - (V2 - V7),
V5 - (V4 + V3 - V8),
]
[4]:
sol = sympy.solve(eqs, unknowns)
sol
[4]:
$$\left \{ C : \frac{G_{1} G_{3} R \left(G_{2} + 1\right)}{G_{1} G_{2} G_{3} H_{1} H_{3} + G_{1} G_{2} H_{1} + G_{2} G_{3} H_{2} H_{3} + G_{2} H_{2} + G_{3} H_{3} + 1}, \quad V_{1} : \frac{R \left(G_{2} H_{2} + 1\right)}{G_{1} G_{2} H_{1} + G_{2} H_{2} + 1}, \quad V_{2} : \frac{G_{1} R \left(G_{2} H_{2} + 1\right)}{G_{1} G_{2} H_{1} + G_{2} H_{2} + 1}, \quad V_{3} : \frac{G_{1} R}{G_{1} G_{2} H_{1} + G_{2} H_{2} + 1}, \quad V_{4} : \frac{G_{1} G_{2} R}{G_{1} G_{2} H_{1} + G_{2} H_{2} + 1}, \quad V_{5} : \frac{G_{1} R \left(G_{2} + 1\right)}{G_{1} G_{2} G_{3} H_{1} H_{3} + G_{1} G_{2} H_{1} + G_{2} G_{3} H_{2} H_{3} + G_{2} H_{2} + G_{3} H_{3} + 1}, \quad V_{6} : \frac{G_{1} G_{2} H_{1} R}{G_{1} G_{2} H_{1} + G_{2} H_{2} + 1}, \quad V_{7} : \frac{G_{1} G_{2} H_{2} R}{G_{1} G_{2} H_{1} + G_{2} H_{2} + 1}, \quad V_{8} : \frac{G_{1} G_{3} H_{3} R \left(G_{2} + 1\right)}{G_{1} G_{2} G_{3} H_{1} H_{3} + G_{1} G_{2} H_{1} + G_{2} G_{3} H_{2} H_{3} + G_{2} H_{2} + G_{3} H_{3} + 1}\right \}$$
The solution in the notes is factored:
[5]:
sol[C].factor()
[5]:
$$\frac{G_{1} G_{3} R \left(G_{2} + 1\right)}{\left(G_{3} H_{3} + 1\right) \left(G_{1} G_{2} H_{1} + G_{2} H_{2} + 1\right)}$$