1. The draining cup problem

In this notebook we will be modelling a draining cup. We assume the cup is shaped like a conical frustrum or truncated cone:

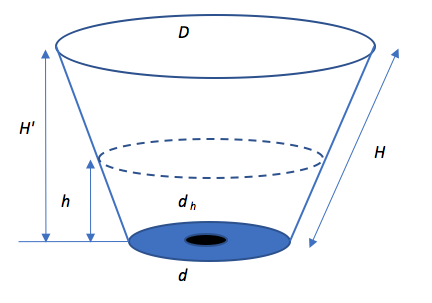
\(D\) and \(d\) are the top and bottom diameters of the cup, \(H\) is the side length between the diameters, \(d_h\) is the hole diameter. We also define \(H'\) as the vertical height of the cup and \(h\) as the vertical height (or level) of the liquid in the cup

1.1. Volume-height relationship

Let’s work out the relationship between the volume of water and the level in the cup by integrating the area:

\[V = \int_0^h A(h) dh\]

import sympy
sympy.init_printing()

D, d, H, h = sympy.symbols('D, d, H, h', real=True)

R = D/2
r = d/2
Hprime = sympy.sqrt(H**2 - (R - r)**2)  # Pythagoras

The radius changes linearly from the small one to the large one:

radius = r + h/Hprime*(R - r)

Now it is easy to calculate the area:

A = sympy.pi*radius**2

And from there, the volume:

V = sympy.integrate(A, (h, 0, h))

V

$$\frac{\pi d^{2} h}{4} - \frac{h^{3} \left(\pi D^{2} - 2 \pi D d + \pi d^{2}\right)}{3 D^{2} - 6 D d - 12 H^{2} + 3 d^{2}} - \frac{h^{2} \left(- \pi D d + \pi d^{2}\right)}{2 \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}}$$

print(V)

pi*d**2*h/4 - h**3*(pi*D**2 - 2*pi*D*d + pi*d**2)/(3*D**2 - 6*D*d - 12*H**2 + 3*d**2) - h**2*(-pi*D*d + pi*d**2)/(2*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2))

1.2. Dynamic model

The basic model of the cup we will be working with looks something like this:

\begin{align} \frac{dV}{dt} &= -F_{\text{out}} & \text{Mass Balance simplified to volume balance} \\ F_{\text{out}} &= f(h) & \text{Hydraulics} \\ h &= f(V) & \text{Geometry} \\ \end{align}

The above geometric description allows us to find the \(V(h)\), but we actually want \(h(V)\).

Vsymb = sympy.symbols('V', real=True)

hV = sympy.solve(Vsymb - V, h)

hV

$$\left [ - \frac{- \frac{3 \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{4 D^{2} - 8 D d + 4 d^{2}} + \frac{\left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{2}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{2}}}{3 \sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{4 D^{2} - 8 D d + 4 d^{2}} + \frac{\left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{2}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{2}}\right)^{3} + \left(\frac{27 \left(3 D^{2} V - 6 D V d - 12 H^{2} V + 3 V d^{2}\right)}{\pi D^{2} - 2 \pi D d + \pi d^{2}} - \frac{9 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right) \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right) \left(4 D^{2} - 8 D d + 4 d^{2}\right)} + \frac{2 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{3}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{3}}\right)^{2}}}{2} + \frac{27 \left(3 D^{2} V - 6 D V d - 12 H^{2} V + 3 V d^{2}\right)}{2 \left(\pi D^{2} - 2 \pi D d + \pi d^{2}\right)} - \frac{9 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right) \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{2 \left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right) \left(4 D^{2} - 8 D d + 4 d^{2}\right)} + \frac{\left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{3}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{3}}}} - \frac{\sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{4 D^{2} - 8 D d + 4 d^{2}} + \frac{\left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{2}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{2}}\right)^{3} + \left(\frac{27 \left(3 D^{2} V - 6 D V d - 12 H^{2} V + 3 V d^{2}\right)}{\pi D^{2} - 2 \pi D d + \pi d^{2}} - \frac{9 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right) \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right) \left(4 D^{2} - 8 D d + 4 d^{2}\right)} + \frac{2 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{3}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{3}}\right)^{2}}}{2} + \frac{27 \left(3 D^{2} V - 6 D V d - 12 H^{2} V + 3 V d^{2}\right)}{2 \left(\pi D^{2} - 2 \pi D d + \pi d^{2}\right)} - \frac{9 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right) \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{2 \left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right) \left(4 D^{2} - 8 D d + 4 d^{2}\right)} + \frac{\left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{3}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{3}}}}{3} - \frac{3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}}{3 \left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)}, \quad - \frac{- \frac{3 \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{4 D^{2} - 8 D d + 4 d^{2}} + \frac{\left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{2}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{2}}}{3 \left(- \frac{1}{2} - \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{4 D^{2} - 8 D d + 4 d^{2}} + \frac{\left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{2}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{2}}\right)^{3} + \left(\frac{27 \left(3 D^{2} V - 6 D V d - 12 H^{2} V + 3 V d^{2}\right)}{\pi D^{2} - 2 \pi D d + \pi d^{2}} - \frac{9 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right) \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right) \left(4 D^{2} - 8 D d + 4 d^{2}\right)} + \frac{2 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{3}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{3}}\right)^{2}}}{2} + \frac{27 \left(3 D^{2} V - 6 D V d - 12 H^{2} V + 3 V d^{2}\right)}{2 \left(\pi D^{2} - 2 \pi D d + \pi d^{2}\right)} - \frac{9 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right) \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{2 \left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right) \left(4 D^{2} - 8 D d + 4 d^{2}\right)} + \frac{\left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{3}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{3}}}} - \frac{\left(- \frac{1}{2} - \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{4 D^{2} - 8 D d + 4 d^{2}} + \frac{\left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{2}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{2}}\right)^{3} + \left(\frac{27 \left(3 D^{2} V - 6 D V d - 12 H^{2} V + 3 V d^{2}\right)}{\pi D^{2} - 2 \pi D d + \pi d^{2}} - \frac{9 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right) \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right) \left(4 D^{2} - 8 D d + 4 d^{2}\right)} + \frac{2 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{3}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{3}}\right)^{2}}}{2} + \frac{27 \left(3 D^{2} V - 6 D V d - 12 H^{2} V + 3 V d^{2}\right)}{2 \left(\pi D^{2} - 2 \pi D d + \pi d^{2}\right)} - \frac{9 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right) \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{2 \left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right) \left(4 D^{2} - 8 D d + 4 d^{2}\right)} + \frac{\left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{3}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{3}}}}{3} - \frac{3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}}{3 \left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)}, \quad - \frac{- \frac{3 \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{4 D^{2} - 8 D d + 4 d^{2}} + \frac{\left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{2}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{2}}}{3 \left(- \frac{1}{2} + \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{4 D^{2} - 8 D d + 4 d^{2}} + \frac{\left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{2}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{2}}\right)^{3} + \left(\frac{27 \left(3 D^{2} V - 6 D V d - 12 H^{2} V + 3 V d^{2}\right)}{\pi D^{2} - 2 \pi D d + \pi d^{2}} - \frac{9 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right) \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right) \left(4 D^{2} - 8 D d + 4 d^{2}\right)} + \frac{2 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{3}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{3}}\right)^{2}}}{2} + \frac{27 \left(3 D^{2} V - 6 D V d - 12 H^{2} V + 3 V d^{2}\right)}{2 \left(\pi D^{2} - 2 \pi D d + \pi d^{2}\right)} - \frac{9 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right) \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{2 \left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right) \left(4 D^{2} - 8 D d + 4 d^{2}\right)} + \frac{\left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{3}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{3}}}} - \frac{\left(- \frac{1}{2} + \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{4 D^{2} - 8 D d + 4 d^{2}} + \frac{\left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{2}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{2}}\right)^{3} + \left(\frac{27 \left(3 D^{2} V - 6 D V d - 12 H^{2} V + 3 V d^{2}\right)}{\pi D^{2} - 2 \pi D d + \pi d^{2}} - \frac{9 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right) \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right) \left(4 D^{2} - 8 D d + 4 d^{2}\right)} + \frac{2 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{3}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{3}}\right)^{2}}}{2} + \frac{27 \left(3 D^{2} V - 6 D V d - 12 H^{2} V + 3 V d^{2}\right)}{2 \left(\pi D^{2} - 2 \pi D d + \pi d^{2}\right)} - \frac{9 \left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right) \left(- 3 D^{2} d^{2} + 6 D d^{3} + 12 H^{2} d^{2} - 3 d^{4}\right)}{2 \left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right) \left(4 D^{2} - 8 D d + 4 d^{2}\right)} + \frac{\left(3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}\right)^{3}}{\left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)^{3}}}}{3} - \frac{3 D^{2} d - 6 D d^{2} - 12 H^{2} d + 3 d^{3}}{3 \left(- 2 D \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}} + 2 d \sqrt{- D^{2} + 2 D d + 4 H^{2} - d^{2}}\right)}\right ]$$

#print(hV)

-(-3*(-3*D**2*d**2 + 6*D*d**3 + 12*H**2*d**2 - 3*d**4)/(4*D**2 - 8*D*d + 4*d**2) + (3*D**2*d - 6*D*d**2 - 12*H**2*d + 3*d**3)**2/(-2*D*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2) + 2*d*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2))**2)/(3*(sqrt(-4*(-3*(-3*D**2*d**2 + 6*D*d**3 + 12*H**2*d**2 - 3*d**4)/(4*D**2 - 8*D*d + 4*d**2) + (3*D**2*d - 6*D*d**2 - 12*H**2*d + 3*d**3)**2/(-2*D*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2) + 2*d*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2))**2)**3 + (27*(3*D**2*V - 6*D*V*d - 12*H**2*V + 3*V*d**2)/(pi*D**2 - 2*pi*D*d + pi*d**2) - 9*(3*D**2*d - 6*D*d**2 - 12*H**2*d + 3*d**3)*(-3*D**2*d**2 + 6*D*d**3 + 12*H**2*d**2 - 3*d**4)/((-2*D*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2) + 2*d*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2))*(4*D**2 - 8*D*d + 4*d**2)) + 2*(3*D**2*d - 6*D*d**2 - 12*H**2*d + 3*d**3)**3/(-2*D*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2) + 2*d*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2))**3)**2)/2 + 27*(3*D**2*V - 6*D*V*d - 12*H**2*V + 3*V*d**2)/(2*(pi*D**2 - 2*pi*D*d + pi*d**2)) - 9*(3*D**2*d - 6*D*d**2 - 12*H**2*d + 3*d**3)*(-3*D**2*d**2 + 6*D*d**3 + 12*H**2*d**2 - 3*d**4)/(2*(-2*D*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2) + 2*d*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2))*(4*D**2 - 8*D*d + 4*d**2)) + (3*D**2*d - 6*D*d**2 - 12*H**2*d + 3*d**3)**3/(-2*D*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2) + 2*d*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2))**3)**(1/3)) - (sqrt(-4*(-3*(-3*D**2*d**2 + 6*D*d**3 + 12*H**2*d**2 - 3*d**4)/(4*D**2 - 8*D*d + 4*d**2) + (3*D**2*d - 6*D*d**2 - 12*H**2*d + 3*d**3)**2/(-2*D*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2) + 2*d*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2))**2)**3 + (27*(3*D**2*V - 6*D*V*d - 12*H**2*V + 3*V*d**2)/(pi*D**2 - 2*pi*D*d + pi*d**2) - 9*(3*D**2*d - 6*D*d**2 - 12*H**2*d + 3*d**3)*(-3*D**2*d**2 + 6*D*d**3 + 12*H**2*d**2 - 3*d**4)/((-2*D*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2) + 2*d*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2))*(4*D**2 - 8*D*d + 4*d**2)) + 2*(3*D**2*d - 6*D*d**2 - 12*H**2*d + 3*d**3)**3/(-2*D*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2) + 2*d*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2))**3)**2)/2 + 27*(3*D**2*V - 6*D*V*d - 12*H**2*V + 3*V*d**2)/(2*(pi*D**2 - 2*pi*D*d + pi*d**2)) - 9*(3*D**2*d - 6*D*d**2 - 12*H**2*d + 3*d**3)*(-3*D**2*d**2 + 6*D*d**3 + 12*H**2*d**2 - 3*d**4)/(2*(-2*D*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2) + 2*d*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2))*(4*D**2 - 8*D*d + 4*d**2)) + (3*D**2*d - 6*D*d**2 - 12*H**2*d + 3*d**3)**3/(-2*D*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2) + 2*d*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2))**3)**(1/3)/3 - (3*D**2*d - 6*D*d**2 - 12*H**2*d + 3*d**3)/(3*(-2*D*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2) + 2*d*sqrt(-D**2 + 2*D*d + 4*H**2 - d**2)))