1. Standard process inputs
[1]:
import sympy
import matplotlib.pyplot as plt
sympy.init_printing()
%matplotlib inline
1.1. Step
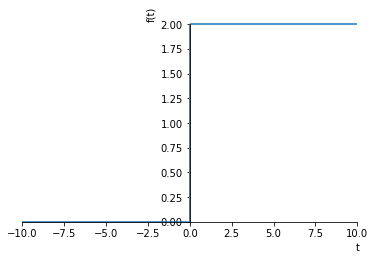
A step input of magnitude \(M\) can be written as
Sympy supplies a unit step function called Heaviside, which is typeset as \(\theta(t)\)
[2]:
t = sympy.symbols('t')
[3]:
S = sympy.Heaviside
[4]:
M = 2
[5]:
sympy.plot(M*S(t))
[5]:
<sympy.plotting.plot.Plot at 0x1178f46a0>
1.2. Laplace transform
Sympy can calculate laplace transforms of the step easily:
[6]:
M, s = sympy.symbols('M, s')
[7]:
def L(f):
return sympy.laplace_transform(f, t, s, noconds=True)
def invL(F):
return sympy.inverse_laplace_transform(F, s, t)
[8]:
L(M*S(t))
[8]:
1.3. Scaling and translation
We can scale and translate the step function in the normal way. Notice that how the time translation is handled.
[9]:
from ipywidgets import interact
[10]:
def translated_step(scale, y_translation, t_translation):
f = scale*S(t - t_translation) + y_translation
print("f =", f, " \u2112(f) =", L(f))
sympy.plot(f, (t, -10, 10), ylim=(-2, 4))
[11]:
interact(translated_step,
scale=(0.5, 3.),
y_translation=(-1., 1.),
t_translation=(0., 5.));
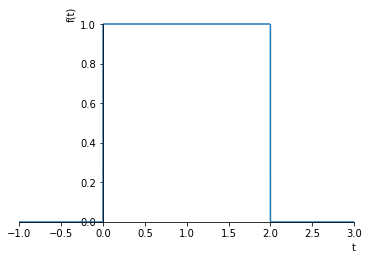
1.4. Rectangular pulse
It is now easy to see how we can construct a rectangular pulse, of height \(h\) and width \(t_w\),
by using shifted versions of the step, so that
[12]:
h, t_w = sympy.symbols('h, t_w')
u_RP = h*(S(t - 0) - S(t - t_w))
[13]:
sympy.plot(u_RP.subs({h: 1, t_w: 2}), (t, -1, 3));
[14]:
L(u_RP)
[14]:
1.4.1. Arbitrary piecewise constant functions
We can constuct any piecewise constant function by adding together step functions shifted in time. As an example, we can take the function represented below:
[15]:
x = [-1, 0, 0, 1, 1, 2, 2, 3]
y = [0, 0, 1, 1, 2, 2, 0, 0]
[16]:
plt.plot(x, y)
plt.text(0, 0.5, r'$\Delta_1=1$')
plt.text(1, 1.5, r'$\Delta_2=1$')
plt.text(2, 1, r'$\Delta_3=-2$')
plt.text(0, 0.1, r'$D_1=0$')
plt.text(1, 0.1, r'$D_2=1$')
plt.text(2, 0.1, r'$D_3=2$')
[16]:
Text(2,0.1,'$D_3=2$')
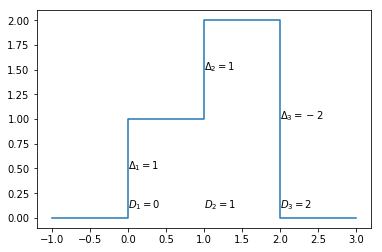
In general piecewise constant functions like the one above can be written as
where \(S\) is the unit step. We calculate \(\Delta_i\) as the difference between the values at the discontinuities, positive if the function is rising and negative if it is falling. \(D_i\) is the time at which the value changes and \(N_d\) is the number of discontinuities.
We can apply this directly for the example function.
[17]:
f = 1*S(t) + 1*S(t-1) - 2*S(t-2)
f
[17]:
Or a little more generally using some code:
[18]:
Delta = [1, 1, -2]
D = [0, 1, 2]
Nd = len(Delta)
[19]:
f = sum(Delta[i]*S(t - D[i]) for i in range(Nd))
[20]:
f
[20]:
Let’s verify it works properly:
[21]:
sympy.plot(f, (t, -1, 3));

[22]:
sympy.expand(L(f))
[22]:
1.5. Ramp
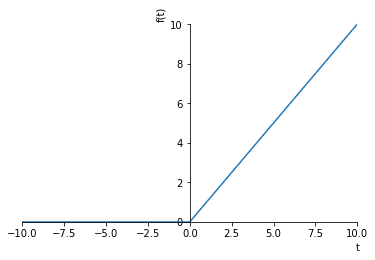
A ramp with slope \(a\) can be written as
We can construct a unit (\(a=1\)) ramp by simply multiplying the unit step by \(t\)
[23]:
def R(t):
return t*S(t)
[24]:
sympy.plot(R(t))
[24]:
<sympy.plotting.plot.Plot at 0x11a539198>
[25]:
L(R(t))
[25]:
1.6. Continuous piecewise linear functions
We can build any continuous piecewise linear function by using shifted and scaled ramps.
This time \(\Delta m_i\) represents changes in slopes (\(m=\frac{\Delta y}{\Delta x}\)). \(D_{s,i}\) are the times at which the slopes change and \(N_s\) is the number of slope changes.
For instance, we can construct a triangular pulse by adding three ramps together.
[26]:
r1 = t*S(t - 0)
r2 = -2*(t - t_w/2)*S(t - t_w/2)
r3 = (t - t_w)*S(t - t_w)
u_TP = 2/t_w*(r1 + r2 + r3)
[27]:
u_TP
[27]:
[28]:
sympy.plot(u_TP.subs({t_w: 2}), (t, -1, 4))
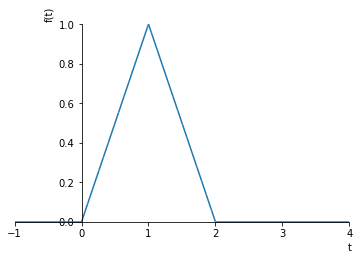
[28]:
<sympy.plotting.plot.Plot at 0x11a6de550>
[29]:
L(u_TP.subs({t_w: 2})).expand()
[29]:
Notice that there are three ramps here (one may have expected only two). It becomes more clear when we think about the derivative of this function:
[30]:
sympy.plot(u_TP.diff(t).subs({t_w: 2}), (t, -1, 4), ylim=(-1.1, 1.1))
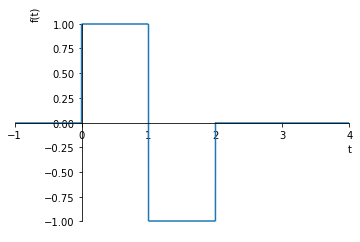
[30]:
<sympy.plotting.plot.Plot at 0x11c5a5710>
We now see that the derivative of a piecewise linear continuous function is a piecewise constant function. We can apply our rule for piecewise constant functions and integrate the steps to ramps:
[31]:
derivative = 1*S(t-0) - 2*S(t-1) + 1*S(t-2)
[32]:
final = 1*R(t-0) - 2*R(t-1) + 1*R(t-2)
1.7. Arbitrary piecewise linear functions
We can construct any piecewise linear function by adding together ramp functions and steps shifted in time. The general rule now becomes
[33]:
x = [-1, 0, 2, 2, 3, 4, 5]
y = [0, 0, 1, 2, 2, 0, 0]
[34]:
plt.plot(x, y)
[34]:
[<matplotlib.lines.Line2D at 0x11ac04d30>]
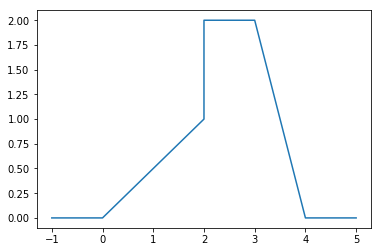
We see that there are 4 slope changes (at t=0, t=2, t=3 and t=4) and 1 discontinuity. Applying our formula yields:
[35]:
g = 0.5*R(t) - 0.5*R(t-2) - 2*R(t-3) + 2*R(t - 4) + S(t - 2)
[36]:
sympy.plot(g, (t, -1, 5));
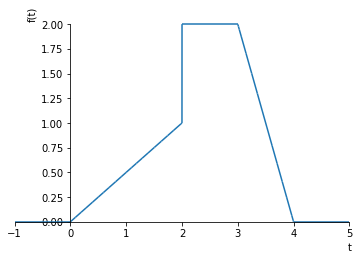
[37]:
sympy.expand(L(g))
[37]: